Motors in any application must be sized using speed and torque, not horsepower.  Horsepower is a rating, while torque is what produces work (motion). 

In motor applications, the torque required is defined as:

T_t = T_a + T_f  

where T_t is the total torque required

T_a is the torque to accelerate the load and

T_f  is the friction torque

Friction torque can be calculated or measured for a given mechanical load.  The torque to accelerate a load is dependent on the load’s inertia, which can only be calculated. 

In applications using AC, DC, or servo motors, inertia concerns are secondary due to the way these motors are controlled.  A simple AC motor in small sizes (below 1HP) is started by applying the current and voltage to the motor via a switch closure.  There are no controls present to limit the current or voltage.  This is referred to as across the line starting.  In this scenario, the motor can draw as much as 700% rated current, allowing 7x the available torque to overcome the load inertia.  In variable speed applications using DC drives, variable frequency AC drives, or servos, current is limited to the motor by the controller, but it still allows for intermittent torque to accelerate the load.

Stepper Motors are unique and are very much limited by the load inertia. 

This is because step motors require a stepper drive to function and by design, these drives supply constant current to the motor.  As a result, there is no intermittent duty range which would allow for increased torque during acceleration.  In applying step motors, care must be taken to supply only the rated current to the motor.

The torque to accelerate a load is given as:

T_a = (J_t)(ΔV/Δt)

J_t is the total inertia (inertia of the load plus the motor)

ΔV/Δt is the load acceleration (change in velocity V divided by the time to accelerate t)

As illustrated by this relationship, there is a direct correlation between inertia and torque.  The higher the inertia, the more torque will be needed.  Higher speeds or reduced acceleration time will also increase the torque requirement.

1.  The motor fails to move as soon as you try to accelerate it.  If the motor grumbles or vibrates, that is an indication the drive is sending it signals, but there is too much inertia.
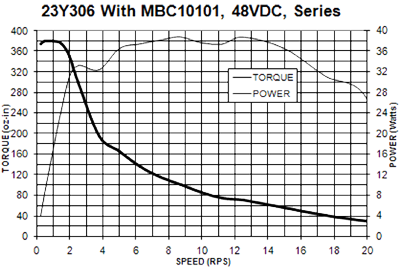
2.  The motor stalls during acceleration.  This also indicates the system is working, but you are running out of torque during acceleration.  Remember, step motors are variable torque, and the torque decreases with higher speeds.

Neither of these issues will cause the motor to burn out since, by design, stepper motors are constant current devices.  The solution in either case is to evaluate the inertia and use a larger motor.  Adding mechanical advantage to your drive train (e.g. a gear reducer/gearbox or a pulley reduction) reduces the reflected load inertia by the square of the reduction.  Care needs to be taken to not use a reduction too large, since there are diminishing returns as the step motor can run out of torque at the higher speed.

To illustrate this, below is a typical speed-torque curve.  Obviously, the torque declines at higher speed:

For more information on the importance of motor inertia ratios, and the mechanical advantage provided by gearing, please see our video Tutorial: Motor Inertia Ratios. In this video, we discuss the basics of inertia ratios with regard to stepper and servo motors, as well measuring mass moment of inertia, with the goal of helping viewers select the appropriate components for their systems.